The Importance of Mathematical Functions

Introduction:

In the realm of mathematics, functions are the building blocks upon which a vast array of mathematical concepts, models, and solutions are constructed. They serve as the bridges between independent and dependent variables, helping us make sense of real-world phenomena and abstract mathematical structures. In this article, we will delve into the fundamental property that distinguishes functions from relations: the one-to-one correspondence between input and output values.

What Is a Function?

Before we delve into the significance of functions, let’s clarify what a function actually is. In mathematics, a function is a way of expressing a relationship between two variables. Now why do we need a way expressing this relationship? Because knowing the relationship between two variables will allow us to predict the outcome for a known situation. The two variables are often called the independent and dependent variables. A function expresses the relationship by assigning each element from a set of independent variables(the domain) to exactly one element in a set of dependent variables (the codomain). These sets can be thought of as containers for the independent (input) and dependent (output) variables of the function.

The One-to-One Correspondence:

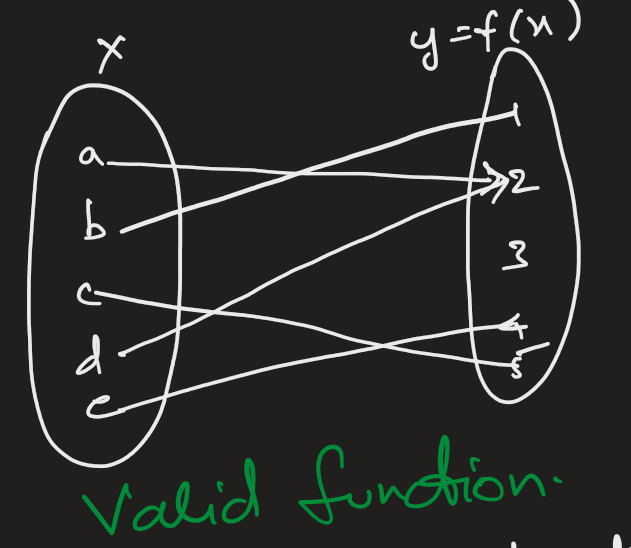
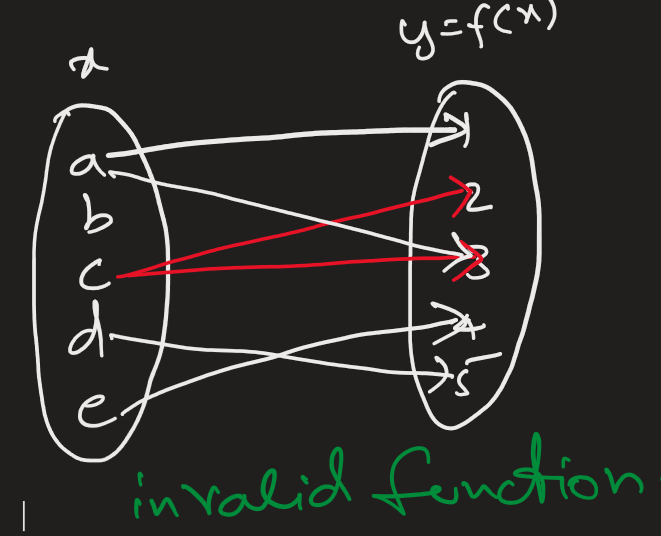
We have understood that functions should be able to help us predict the outcome for a known situation. The outcome has to be a unique one, because if it gives us multiple outcomes the whole purpose is lost. Hence The cornerstone of a function is its one-to-one correspondence, which means that for every known value in the domain, there exists precisely one corresponding value in the codomain. This property is non-negotiable; without it, we do not have a function. The image shows two functions that expresses the relationship between the independent variable X and the dependent variable Y.

In the the First image every element of X is mapped to exactly one element in the set Y. In the second image we can see that element c is mapped to more than one element in the set Y. we have no way of telling whether the value of the function will be 2 or 3 for the input c. Hence the relationship in the second cannot be called as a function.

we understood the one-to-one property of a function.Let’s explore why this property is so crucial:

1. Predictability:

A one-to-one correspondence between inputs and outputs ensures predictability. When you input a specific value, you expect a unique result. This predictability is at the heart of mathematical modeling and problem-solving.

2. Uniqueness of Solutions:

In many mathematical applications, particularly in algebra and calculus, functions are used to model real-world situations. Whether it’s finding the roots of an equation, optimizing a process, or analyzing data trends, functions with a one-to-one relation guarantee that solutions are unique and meaningful.

3. Mathematical Rigor:

Mathematics thrives on precision and rigor. The one-to-one correspondence property adds an essential layer of rigor to functions, allowing mathematicians and scientists to make conclusive statements and proofs based on their work.

4. Real-World Applications:

Functions are not just theoretical constructs; they are applied extensively in fields like physics, engineering, economics, and computer science. In these applications, the one-to-one correspondence property ensures that models accurately represent the systems they describe, leading to better predictions and problem-solving.

Examples and Illustrations:

To better understand the significance of one-to-one correspondence in functions, we’ll explore a few practical examples. We’ll discuss how this property impacts everything from simple linear functions to complex mathematical modeling.

Linear Functions:

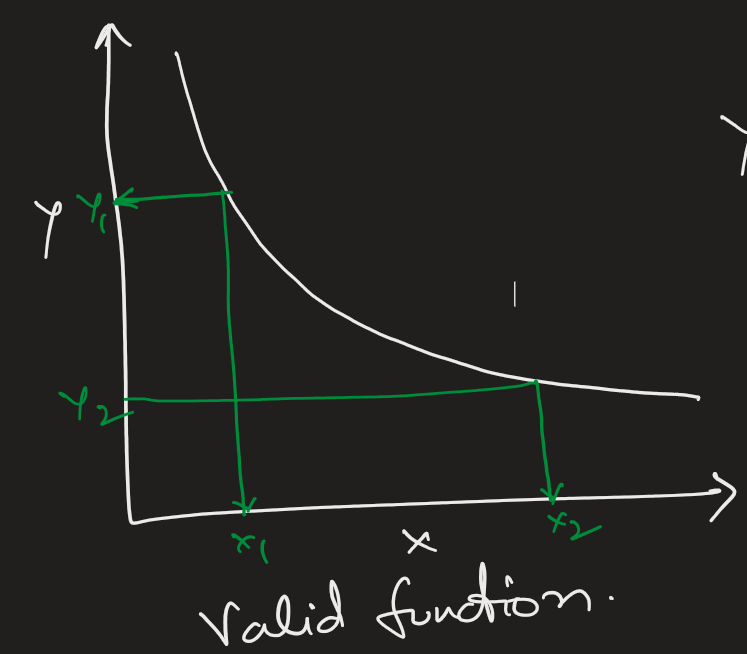
Linear functions, like y = 2x + 3, have a straightforward one-to-one correspondence. For every value of x you input, there’s a unique value of y as output. This simplicity is what allows us to graph lines and make accurate predictions in scenarios ranging from physics to finance. The image below explains the one – to – one property of functions via the graphs.

In the first image we can see that two input values of x1 and x2 will result two unique output values of y1 and y2. In the second image for the input x1, there are two outcomes y1 and y2. Hence the function expressed in the second graph is not a function.

Inverse Functions:

Inverse functions are essentially functions that “reverse” the roles of input and output. The one-to-one correspondence ensures that we can find an inverse function that undoes the original function’s operations, allowing us to solve equations and unravel complex transformations.

Data Analysis:

In data analysis and statistics, functions are used to model relationships between variables. When a function maintains a one-to-one correspondence, it becomes easier to draw meaningful conclusions from data, make predictions, and identify outliers.

Conclusion:

In the world of mathematics, functions with their one-to-one correspondence property are the keys that unlock a multitude of doors, from solving equations to modeling real-world phenomena. This fundamental concept’s significance cannot be overstated, as it ensures predictability, uniqueness, rigor, and applicability in various domains. Whether you’re a student just starting to explore functions or a seasoned mathematician, understanding the importance of this property is essential for success in mathematical endeavors. So, the next time you encounter a function, remember the power of its one-to-one correspondence – the very essence of what makes it a function.